近日,k漫画 k漫画 肖峰教授团队在国际控制领域顶级期刊 IEEE Transactions on Automatic Control 发表了题为“State Estimator Design: Addressing General Delay Structures With Dissipative Constraints”的长文(Full Paper)研究论文。论文刊登于2025年第70卷第7期(4254–4269),DOI:10.1109/TAC.2024.3520835。k漫画 为论文第一完成单位,k漫画 青年教师冯谦为论文第一作者,肖峰教授为通讯作者,博士生王晓宇参与完成了相关研究工作。
具有复杂时滞结构的系统状态估计问题,一直是自动控制理论与工程应用中的难点,在风洞实验、网络化控制、化工过程等实际系统中普遍存在。尤其是在系统同时包含多个点时滞(pointwise delays)和一般化分布时滞(distributed delays)时,积分核函数本身呈现无限维特性,使得在耗散性约束条件下设计观测器面临严峻的理论与计算挑战。现有方法往往依赖较为特殊的系统结构,或者在数值上难以有效求解,推广性和实用性受到显著限制。如何在一般化分布时滞的背景下兼顾分析精度与数值可行性,构造既不保守又鲁棒的估计器,是控制理论领域长期关注的重要科学问题之一。
针对上述问题,k漫画 k漫画 肖峰教授团队在Krasovski泛函(Krasovski functional)框架和二次供给率函数的基础上,提出了一种名为 “Kronecker–Seuret分解(Kronecker–Seuret decomposition, KSD)”的控制概念工具,围绕一般分布时滞系统的状态估计开展了系统研究。借助KSD方法,研究团队给出了对任意分布时滞积分核函数进行分解与逼近的方法,在理论上具有较小的保守性,能够统一处理数量有限但个数不受限制的点时滞,以及具有个数不受限制的平方可积核的一般分布时滞。在此基础上,团队将观测器(估计器)设计问题转化为一组序列凸半正定规划(semidefinite programming, SDP)问题,并设计了离线迭代算法,从而避免了直接依赖非线性数值求解器。相关工作构建了基于 KSD 的 Krasovski 泛函分析框架,并通过数值算例对所提方法在处理由非光滑控制器镇定的时滞系统等复杂场景中的适用性进行了验证,为复杂时滞系统的状态观测与故障诊断提供了一种高效可行的理论工具和计算思路。
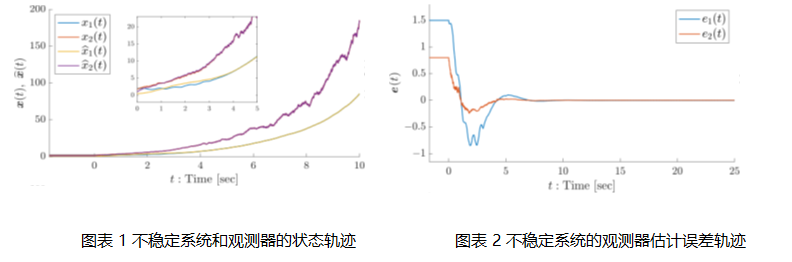
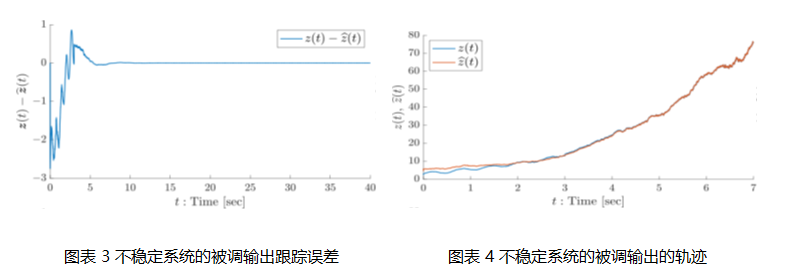
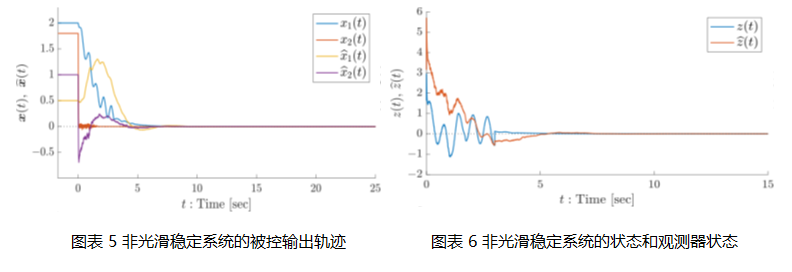
该研究成果得到了国家自然科学基金项目(62303180, 62373150, 62273145)、中央高校基本科研业务费以及法国 ANR-15-CE23-0007 项目的资助。
IEEE Transactions on Automatic Control是IEEE控制系统学会的旗舰汇刊,被公认为国际控制与自动化领域的顶级期刊,是衡量高校控制学科科研水平的重要标志之一。该刊长文发表通常要求在理论方法或工程应用方面具有突出的创新性和较大的突破。
近年来,肖峰教授团队围绕时滞系统、网络化控制与分布式优化等方向持续深耕,系统挖掘相关数学理论在系统分析方面的应用潜力,逐步形成了面向一般化时滞系统以及多智能体系统问题的理论与算法体系。团队依托新能源电力系统国家重点实验室和k漫画 人工智能研究中心,在控制类国际顶级期刊IEEE Transactions系列汇刊、Automatica等发表了一系列高水平学术成果。

初审:肖峰 冯谦
复审:李元诚
审核:董宏伟